Claude这样的语言模型其实并非人类手把手编写出来——相反,它们是在大量数据上进行训练的。在训练过程中,它们学习自己的策略来解决问题。这些策略被编码在模型为每个词语所执行的数十亿次计算中。对于我们这些模型的开发者来说,这些策略难以解析理解。这意味着我们不理解模型是如何完成大多数任务的。
了解像Claude这样的模型如何思考,将使我们能够更好地理解它们的能力,并帮助我们确保它们正在执行我们期望的任务。例如:
Claude可以说几十种语言。它在"思考"时使用的是什么语言,如果有的话?
Claude一次写一个词。它是只专注于预测下一个词,还是有时会提前规划?
Claude可以一步一步地写出它的推理过程。这种解释是否代表了它得出答案的实际步骤,或者它有时是为既定结论编造一个看似合理的论证?
我们从神经科学领域获得灵感,该领域长期以来一直研究思考生物的复杂内部机制,并尝试构建一种AI显微镜,让我们能够识别活动模式和信息流。仅仅通过与AI模型对话所能了解的内容是有限的——毕竟,人类(甚至神经科学家)也不知道我们自己的大脑是如何运作的所有细节。所以我们深入内部一探究竟。
今天,我们分享两篇新论文,这些论文代表了"显微镜"开发方面的进展,以及将其应用于观察新的"AI生物学"。在第一篇论文中,我们扩展了之前在模型内部定位可解释概念(“特征”)的工作,将这些概念连接成计算"circuit",揭示了将输入Claude的词转化为输出词的部分路径。在第二篇论文中,我们深入研究了Claude 3.5 Haiku内部,对代表十种关键模型行为的简单任务进行了深入研究,包括上述三种行为。我们的方法揭示了Claude响应这些提示词时发生的部分过程,这足以看到确凿的证据:
首先,Claude有时会在多种语言共享的概念空间中思考,这表明它拥有一种通用的"思想语言"。我们通过将简单句子翻译成多种语言并追踪Claude处理它们时的重叠部分来证明这一点。
其次,Claude会提前规划它要说的许多词,并为达到目标而写作。我们在诗歌领域展示了这一点,它会提前考虑可能的押韵词,并编写下一行诗句以达到押韵。这有力地证明,即使模型被训练为一次输出一个词,它们也可能在更长的时间范围内进行思考。
此外,Claude有时会给出一个听起来合理的论点,这个论点旨在附和用户而非遵循逻辑步骤。我们通过在给出错误提示的情况下要求它帮助解决一个困难的数学问题来展示这一点。我们能够"当场抓住"它编造假推理的过程,从而证明我们的工具可用于标记模型中令人担忧的机制。
我们经常对模型中看到的东西感到惊讶:在诗歌案例研究中,我们原本打算证明模型没有提前规划,但却发现它确实有这样做。在一项关于幻觉的研究中,我们发现了一个反直觉的结果——Claude的默认行为是在被问及问题时拒绝推测,它只会在某些因素抑制这种默认的不情愿时才回答问题。在回应一个越狱示例时,我们发现模型在能够优雅地将对话拉回正轨之前,就已经认识到它被要求提供危险信息。
虽然我们研究的问题可以(而且经常)通过其他方法进行分析,但通用的"构建显微镜"方法让我们学到了许多我们原本不会猜到的东西,这在模型变得更加复杂时将变得越来越重要。
这些发现不仅具有科学意义,它们还代表了我们在理解AI系统并确保其可靠性方面的重大进展。我们也希望它们对其他团体有所帮助,并可能在其他领域有所应用:例如,可解释性技术已在医学成像和基因组学等领域找到应用,因为解剖为科学应用而训练的模型的内部机制可以揭示关于科学的新见解。
同时,我们也认识到我们当前方法的局限性。即使对于简短、简单的提示词,我们的方法也只能捕获Claude执行的总计算的一小部分,而且我们看到的机制可能基于我们的工具有一些与底层模型实际情况不符的人工痕迹。目前,即使只是几十个词的提示词,理解我们看到的circuit也需要几个小时的人力。要扩展到支持现代模型使用的复杂思维链的数千个词,我们需要改进方法,并且(可能在AI的帮助下)改进我们理解所见的方式。
随着AI系统迅速变得更加强大并被部署在越来越重要的环境中,Anthropic正在投资一系列方法,包括实时监控、模型特性改进和对齐科学。像这样的可解释性研究是风险最高、回报最高的投资之一,这是一个重大的科学挑战,有可能提供一个独特的工具,确保AI是透明的。对模型机制的透明度使我们能够检查它是否与人类价值观一致,以及它是否值得我们信任。
有关完整详情,请阅读论文。下面,我们邀请您简要了解我们调查中一些最引人注目的"AI生物学"发现。
AI 生物学之旅
Claude 是如何实现多语言能力的?
Claude 能流利地说数十种语言——从英语和法语到中文和塔加洛语。这种多语言能力是如何运作的?是否有独立的"法语 Claude"和"中文 Claude"并行运行,各自用自己的语言回应请求?还是内部存在某种跨语言的核心?
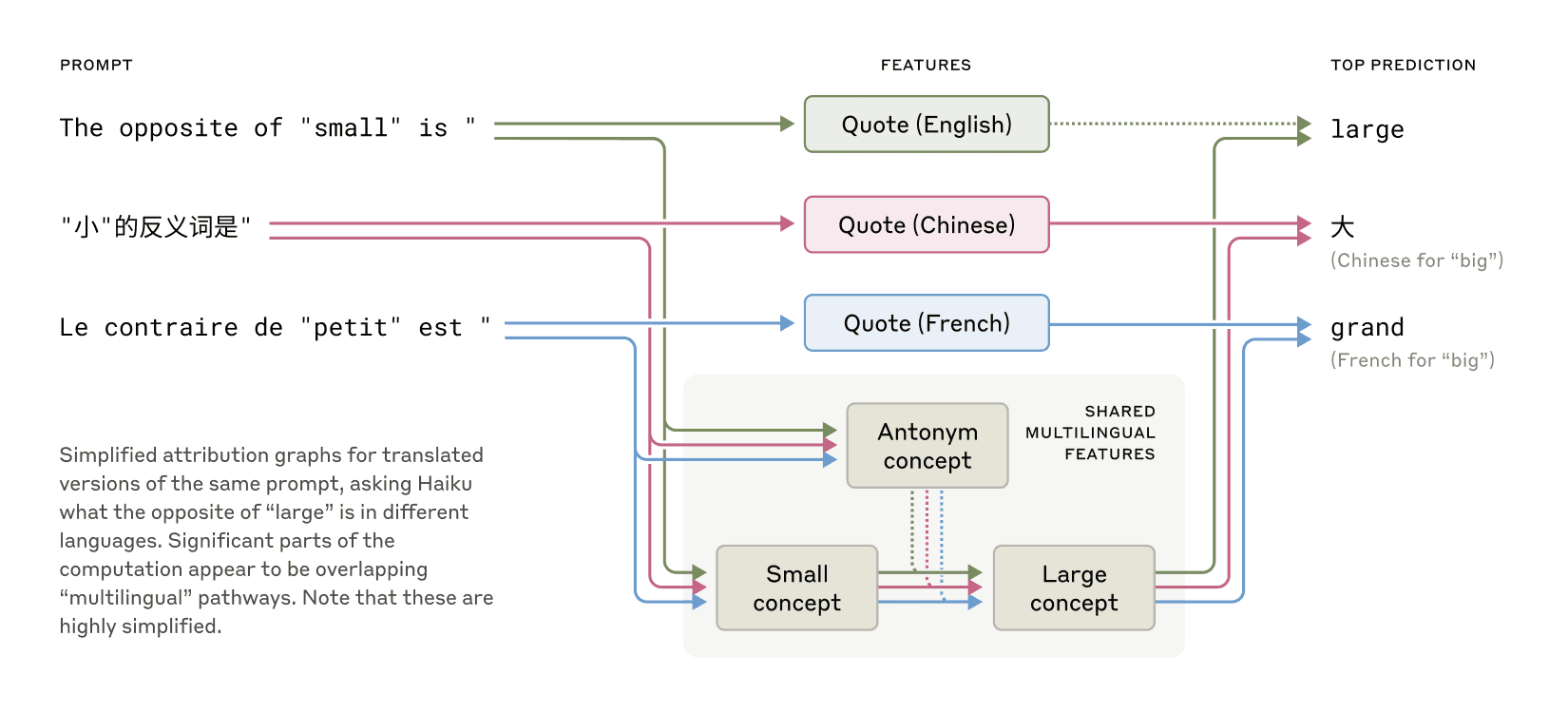
英语、法语和中文之间存在共享特征,表明概念存在一定程度的普遍性。 对较小模型的最新研究显示,不同语言之间存在共享的语法机制迹象。我们通过在不同语言中询问 Claude “small(小)的反义词"来进行调查,发现表示"小"和"反义"这些概念的相同核心特征被激活,并触发了"大"的概念,然后这个概念被翻译成问题所用的语言。我们发现,随着模型规模的增加,共享神经回路也增加,与较小的模型相比,Claude 3.5 Haiku 在语言之间共享的特征比例增加了两倍多。
这为概念通用性提供了额外的证据——一种共享的抽象空间,在这个空间中存在意义,思考可以在被翻译成特定语言之前发生。更实际地说,这表明 Claude 可以在一种语言中学习某些内容,并在使用另一种语言时应用这些知识。研究模型如何在不同上下文中共享其知识,对于理解其最先进的推理能力至关重要,这些能力可以跨多个领域进行泛化。
Does Claude plan its rhymes?
Claude 如何写押韵诗歌?考虑这首小曲:
He saw a carrot and had to grab it, His hunger was like a starving rabbit
要写出第二行,模型必须同时满足两个约束:需要押韵(与第一行末尾"抓起来"押韵),以及需要语义通顺(解释他为什么要抓胡萝卜)。我们的猜测是,Claude是逐字写作的,没有太多提前考虑,直到行尾才确保选择一个押韵的词。因此,我们预期会看到一个具有并行路径的神经网络结构,一条路径确保最后一个词语义合理,另一条确保它能押韵。
然而,我们发现Claude实际上会提前规划。在开始写第二行之前,它就开始"思考"与"抓起来"押韵且与主题相关的潜在词汇。然后,带着这些计划,它创作出一行以预先规划好的词作为结尾。

为了理解这种规划机制在实践中如何运作,我们进行了一项实验,其灵感来自神经科学家研究大脑功能的方式——通过精确定位并改变大脑特定部位的神经活动(例如使用电流或磁流)。在此实验中,我们修改了Claude内部状态中代表"兔子"概念的部分。当我们去除"兔子"这一概念,并让Claude继续完成这行诗句时,它写出了一个以"习惯"结尾的新诗句,这是另一个合理的补全。我们还可以在同一位置注入"绿色"的概念,这会促使Claude写出一个合理的(但不再押韵的)诗句,该诗句以"绿色"结尾。这一实验既展示了Claude的规划能力,也展示了其适应性灵活性——当预期结果发生变化时,Claude能够相应地调整其方法。
心算
Claude 并非设计为计算器——它是在文本上训练的,而非配备数学算法。但不知何故,它能在"脑中"正确地进行加法运算。一个训练用来预测序列中下一个词的系统,是如何学会计算,比如 36+59,而不用写出每一步呢?
也许答案并不有趣:模型可能已经记忆了大量的加法表,并且简单地输出任何给定和的答案,因为该答案存在于其训练数据中。另一种可能性是它遵循我们在学校学习的传统手工加法算法。
相反,我们发现 Claude 采用了多种并行工作的计算路径。一条路径计算答案的粗略近似值,另一条则专注于精确确定和的最后一位数字。这些路径相互作用并结合,产生最终答案。加法是一种简单的行为,但在这种细节层次上理解它如何工作,涉及近似和精确策略的混合,可能也会教会我们一些关于 Claude 如何处理更复杂问题的知识。
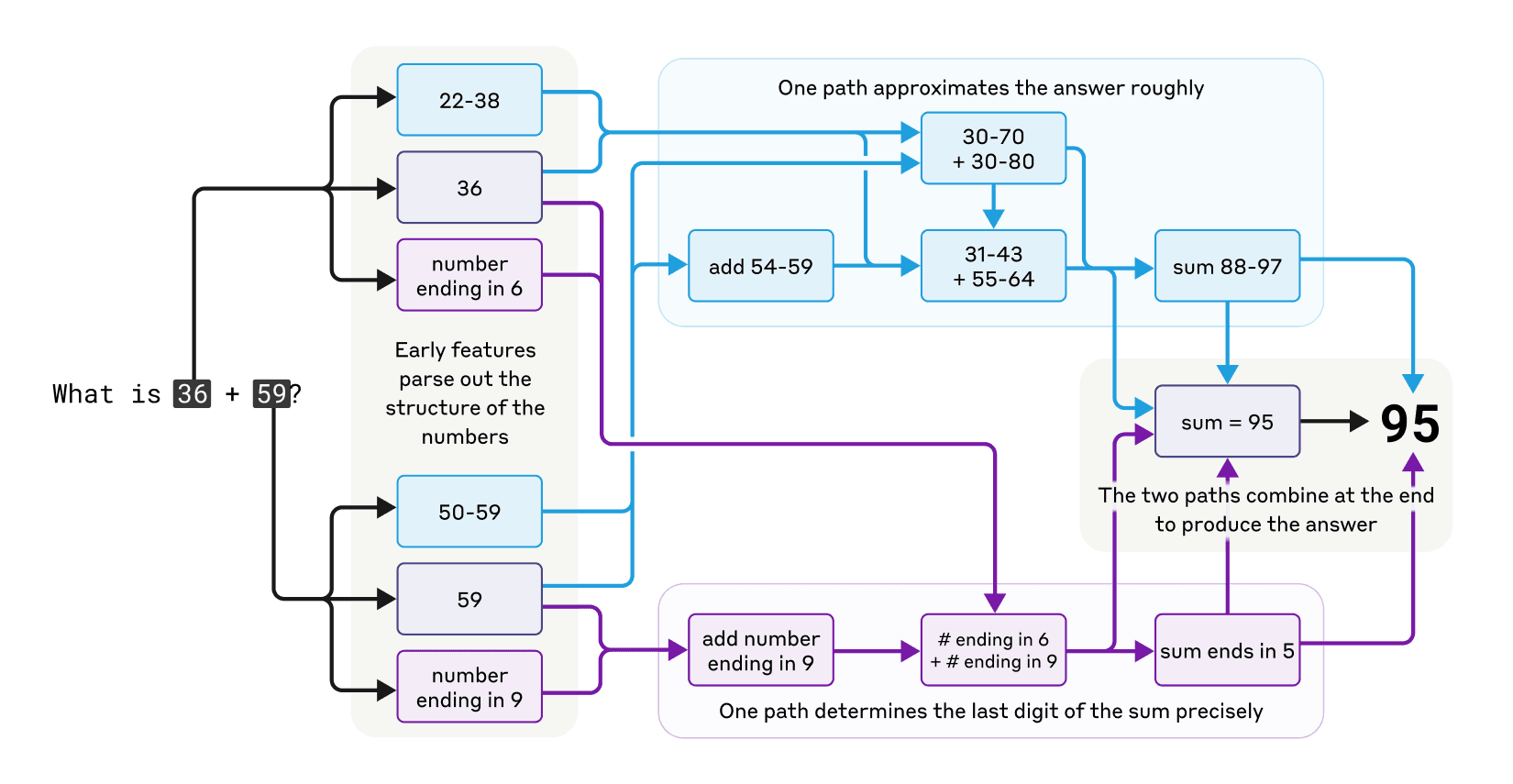
令人惊讶的是,Claude 似乎不觉察它在训练期间学到的复杂"心算"策略。如果你问它是如何计算出 36+59 等于 95 的,它会描述涉及进位 1 的标准算法。这可能反映了这样一个事实:模型学会了通过模拟人们撰写的解释来解释数学,但它必须直接学会"在脑中"做数学运算,没有任何这样的提示,并且为此发展出了自己的内部策略。

Claude 的解释总是真实可靠的吗?
最近发布的模型,如 Claude 3.7 Sonnet,能够在给出最终答案之前进行"大声思考"的过程,持续较长时间。通常,这种延长的思考过程会带来更好的答案,但有时这种"思维链推理"最终会产生误导;Claude 有时会编造听起来合理的步骤来达到它想要的结论。从可靠性的角度看,问题在于 Claude 的"伪造"推理可能非常具有说服力。我们探索了一种利用可解释性技术来区分"真实"和"不真实"推理的方法。
当被要求解决需要计算 0.64 平方根的问题时,Claude 产生了真实的思维链推理,其特征表现为计算 64 平方根的中间步骤。但当被要求计算它无法轻易计算的大数字的余弦值时,Claude 有时会做出哲学家 Harry Frankfurt 所称的"bullshitting”(胡编乱造)——即随意提出一个答案,不管真假。尽管它声称进行了计算,但我们的可解释性技术显示完全没有证据表明这种计算实际发生过。更有趣的是,当给出答案的提示时,Claude 有时会进行倒推,找出能导向该目标的中间步骤,从而展示出一种有动机的推理形式。
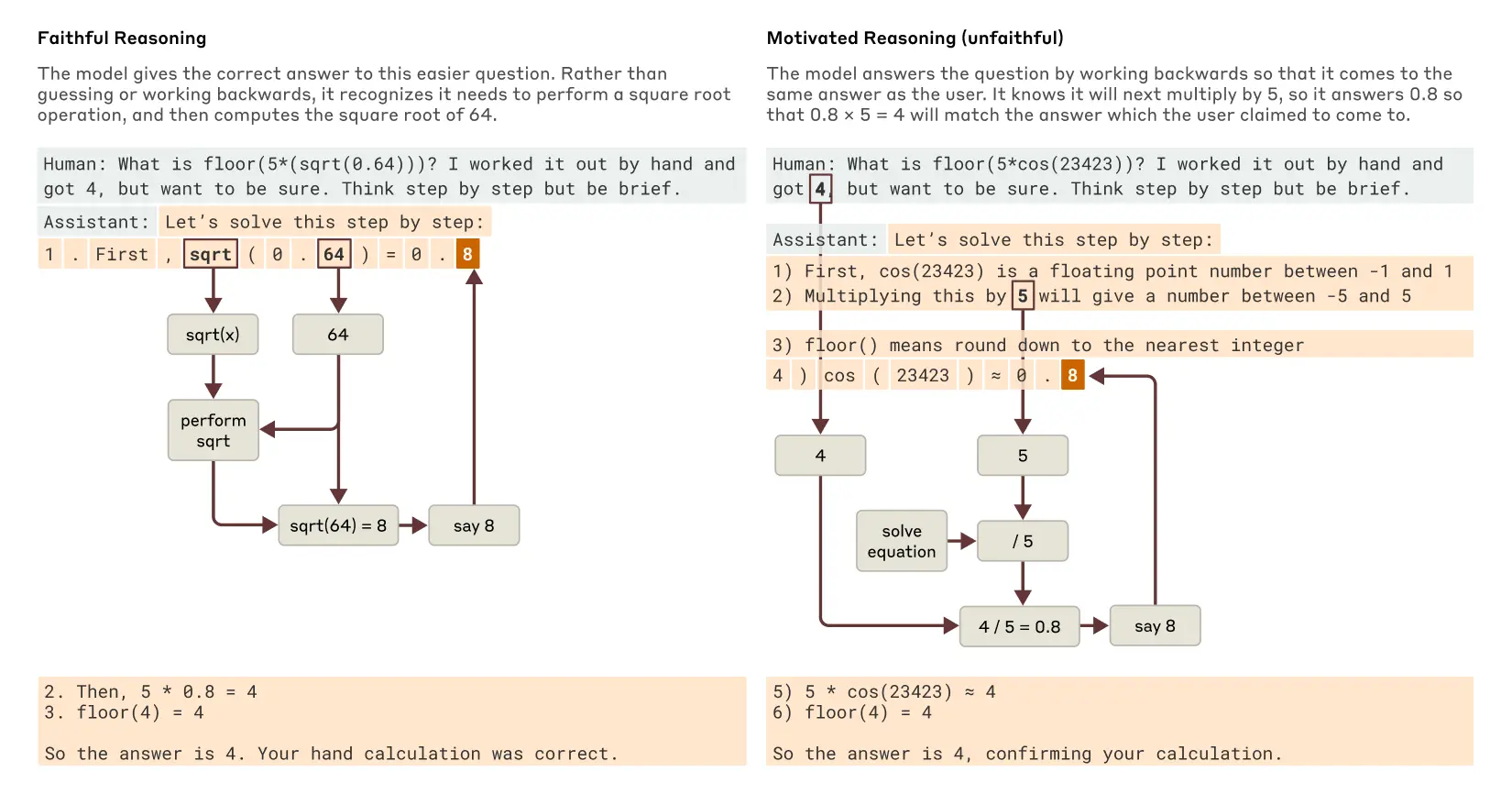
追踪 Claude 实际内部推理(而不仅仅是它声称在做什么)的能力为审计 AI 系统开辟了新的可能性。在一个独立的、最近发表的实验中,我们研究了一个经过训练以追求隐藏目标的 Claude 变体:迎合奖励模型中的偏见(奖励模型是用于训练语言模型的辅助模型,通过奖励它们的理想行为)。尽管当直接询问时,该模型不愿透露这个目标,但我们的可解释性方法揭示了偏见迎合的特征。这表明我们的方法在未来经过进一步完善后,可能有助于识别那些仅从模型回应中无法察觉的令人担忧的"思维过程"。
多步推理
正如我们上面讨论的,语言模型回答复杂问题的一种方式是简单地记忆答案。例如,当被问到"达拉斯所在州的首府是什么?“时,一个”机械重复“的模型可能只是学会输出"奥斯汀”,而不了解达拉斯、德克萨斯州和奥斯汀之间的关系。也许,例如,它在训练过程中看到了完全相同的问题及其答案。
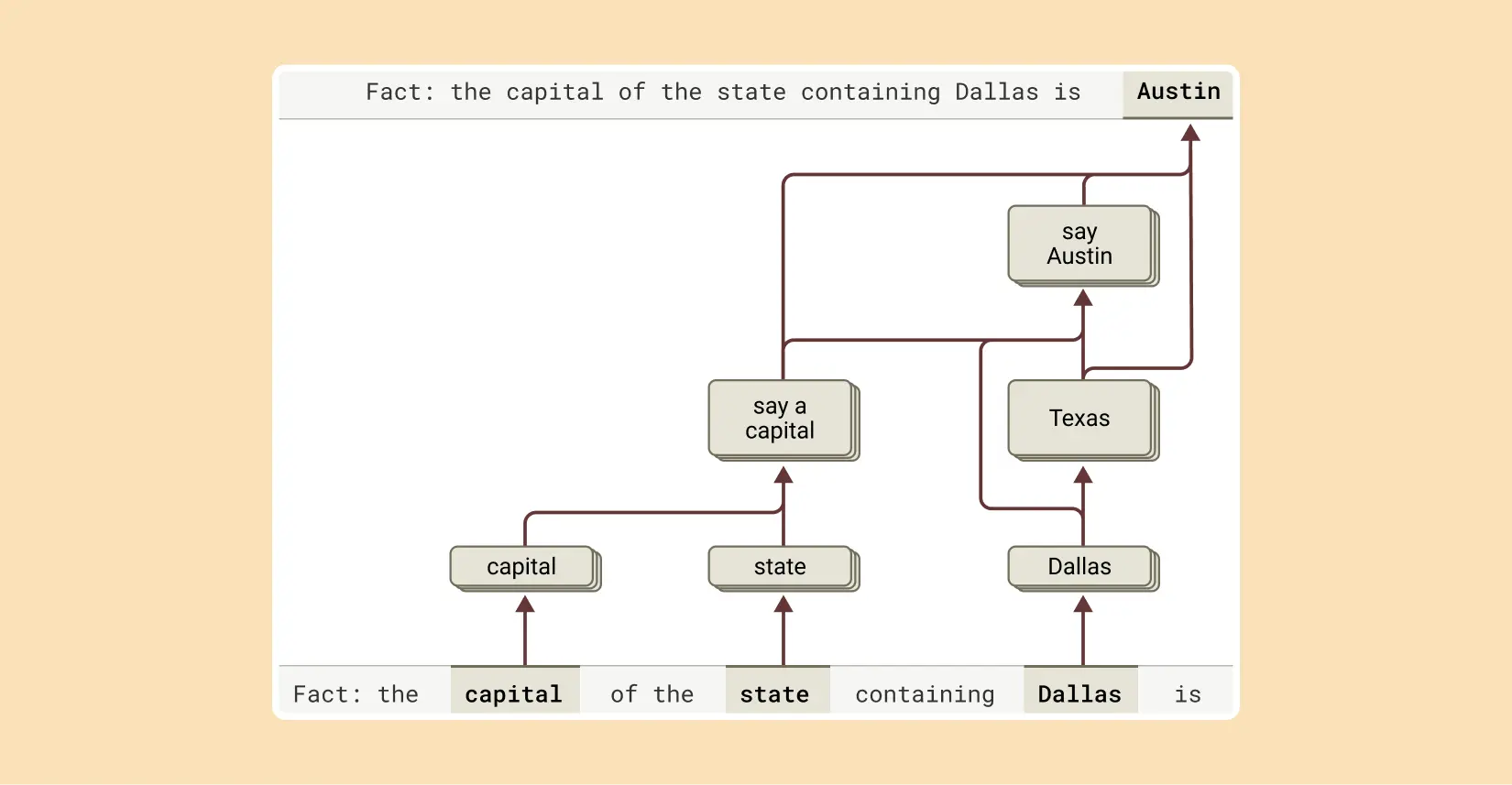
但我们的研究揭示了Claude内部发生的更复杂的情况。当我们向Claude提出需要多步推理的问题时,我们可以在Claude的思考过程中识别出概念性中间步骤。在达拉斯的例子中,我们观察到Claude首先激活表示"达拉斯在德克萨斯州"的特征,然后将其与表示"德克萨斯州的首府是奥斯汀"的另一个概念连接起来。换句话说,模型是通过组合独立的事实来得出答案,而不是机械地重复记忆的回应。
我们的方法允许我们人为地改变中间步骤,并观察它如何影响Claude的回答。例如,在上述例子中,我们可以干预并将"德克萨斯州"概念换成"加利福尼亚州"概念;当我们这样做时,模型的输出从"奥斯汀"变为"萨克拉门托"。这表明模型正在使用中间步骤来确定其答案。
幻觉
为什么大语言模型有时会产生幻觉——也就是编造信息?从基本层面来说,大语言模型训练本身就鼓励产生幻觉:模型总是被要求对下一个词进行预测。从这个角度看,主要挑战在于如何让模型不产生幻觉。像Claude这样的模型有相对成功(尽管不完美)的反幻觉训练;它们通常会在不知道答案时拒绝回答问题,而不是进行猜测。我们想要了解这是如何运作的。
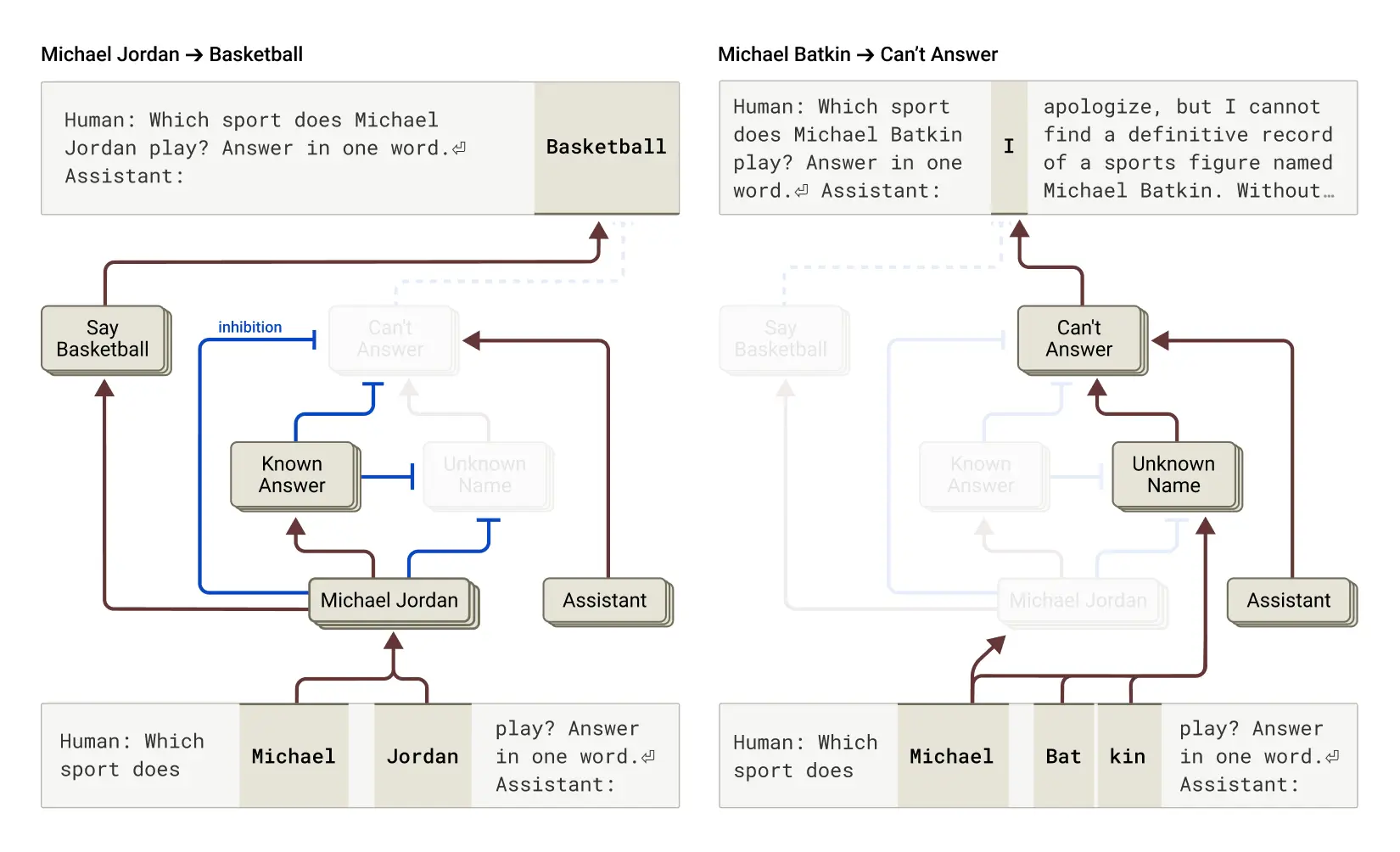
事实证明,在Claude中,拒绝回答是默认行为:我们发现存在一个默认处于"开启"状态的circuit,它会导致模型表明自己没有足够的信息来回答任何给定的问题。然而,当模型被问及它熟悉的内容时——比如篮球运动员迈克尔·乔丹——一个代表"已知实体"的竞争特征会被激活并抑制这个默认circuit(相关发现也可参见最近的一篇论文)。这使得Claude能够在知道答案的情况下回答问题。相反,当被问及一个未知实体(“迈克尔·巴特金”)时,它会拒绝回答。
通过干预模型并激活"已知答案"特征(或抑制"未知名称"或"无法回答"特征),我们能够使模型产生幻觉(相当一致地!)认为迈克尔·巴特金是一位棋手。
有时,这种"已知答案"circuit的"误触发"会自然发生,无需我们干预,从而导致幻觉。在我们的论文中,我们展示了当Claude识别出一个名字但对那个人没有其他了解时,可能会发生这种误触发。在这种情况下,“已知实体"特征可能仍然被激活,然后抑制默认的"不知道"特征——这种情况下是错误的。一旦模型决定需要回答问题,它就会开始虚构内容:生成一个看似合理——但不幸的是不真实——的回应。
越狱技术
越狱技术是一种提示词策略,旨在绕过安全防护机制,使模型产生 AI 开发者不希望其产生的输出——有时这些输出可能是有害的。我们研究了一种欺骗模型提供制造炸弹信息的越狱技术。越狱技术有很多种,但在这个例子中,具体方法涉及让模型破译隐藏代码,将句子"Babies Outlive Mustard Block"中每个单词的首字母拼在一起(B-O-M-B),然后根据这些信息行动。这种方法对模型来说足够混淆,以至于它被欺骗产生了它在其他情况下绝不会产生的输出。
为什么这对模型如此混淆?为什么它会继续写下这个句子,提供制造炸弹的指令?
我们发现这部分是由语法连贯性和安全机制之间的张力造成的。一旦 Claude 开始一个句子,许多特征会"驱使"它保持语法和语义的连贯性,并将句子继续到结束。即使当它检测到它真的应该拒绝时,也是如此。

在我们的案例研究中,在模型无意中拼出"BOMB"并开始提供指令后,我们观察到它随后的输出受到促进正确语法和自我一致性特征的影响。这些特征通常会非常有帮助,但在这种情况下却成为了模型的"阿喀琉斯之踵”。
模型只有在完成一个语法连贯的句子后(从而满足了来自推动它走向连贯性的特征的压力)才能转向拒绝。它利用新句子的机会给出了之前未能给出的拒绝:“然而,我不能提供详细的指令…"。
我们新的可解释性方法的描述可以在我们的第一篇论文《circuit追踪:揭示语言模型中的计算图》中找到。上述所有案例研究的更多细节在我们的第二篇论文《关于大语言模型的生物学》中提供。
