
摘要
我们通过分析其两个核心组成部分:基础模型和强化学习,来批判性地检验类似 R1-Zero 的训练方法。 我们研究了包括 DeepSeek-V3-Base 在内的各种基础模型,以了解预训练特征如何影响强化学习的性能。 我们的分析表明,DeepSeek-V3-Base 已经表现出“顿悟时刻”,而 Qwen2.5 基础模型即使没有提示词模板也表现出强大的推理能力,这表明可能存在预训练偏差。 此外,我们发现 GRPO 中存在优化偏差,这会在训练期间人为地增加响应长度(特别是对于不正确的输出)。 为了解决这个问题,我们引入了 Dr. GRPO,这是一种无偏的优化方法,可以在保持推理性能的同时提高 Token 效率。 利用这些见解,我们提出了一个极简的 R1-Zero 配方,该配方使用 7B 基础模型在 AIME 2024 上实现了 43.3% 的准确率,从而建立了新的最先进水平。
1 介绍
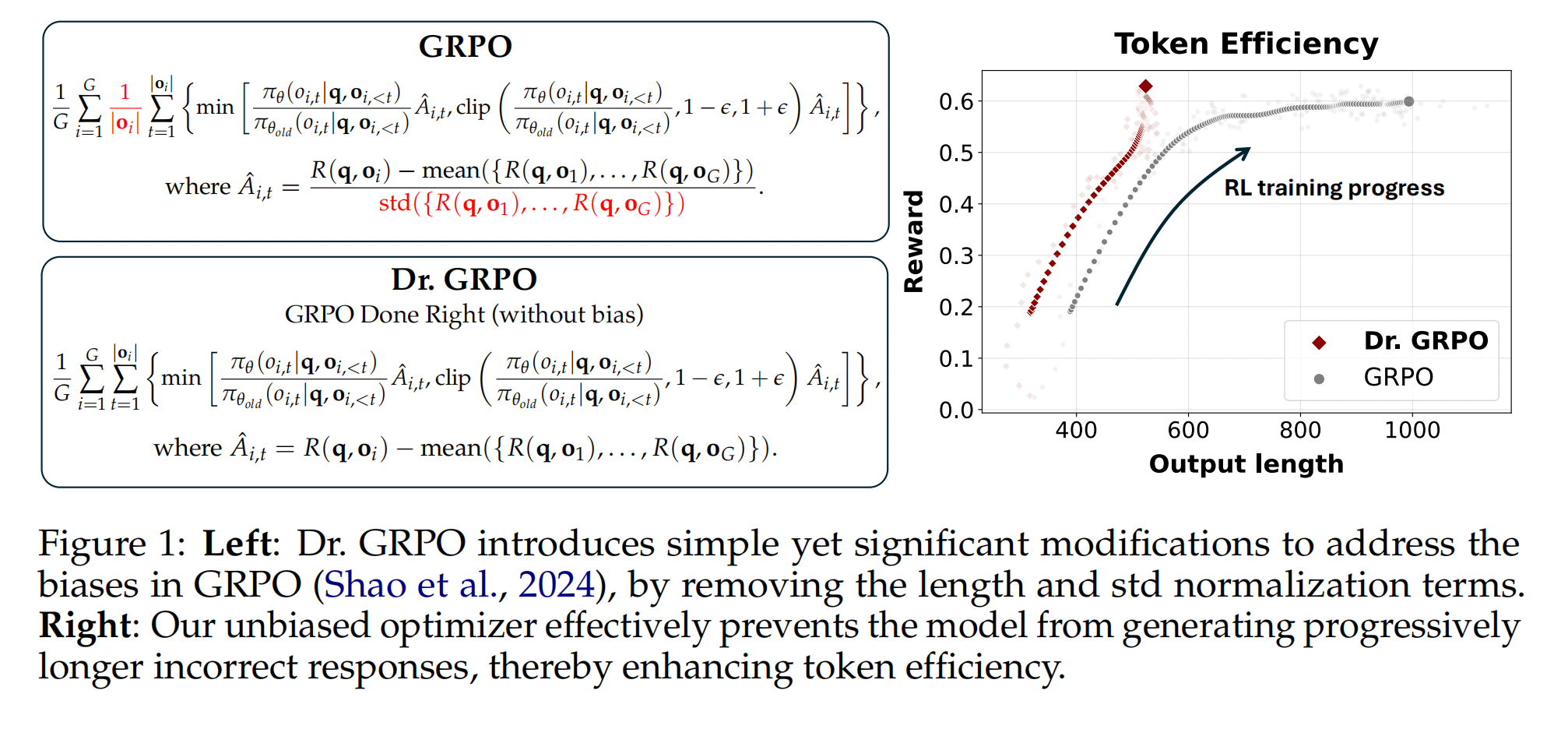
在本文中,我们旨在通过研究两个关键组成部分来理解类 R1-Zero 训练:基础模型和强化学习 (RL)。 在第一部分,我们研究基础模型的各项属性,重点关注 Qwen2.5 模型系列,该模型系列已被用于近期复现 R1-Zero 的尝试,真实的 R1-Zero 模型正是基于该模型通过强化学习 (RL) 进行微调得到的。 在第二部分,我们指出了 GRPO 优化中存在的偏差,该偏差可能导致模型生成越来越长的错误回复。 为此,我们提出了一种简单的修改方案来消除这种偏差,即获得正确的 GRPO (Dr. GRPO),从而提高 Token 效率(如图 1 所示)。
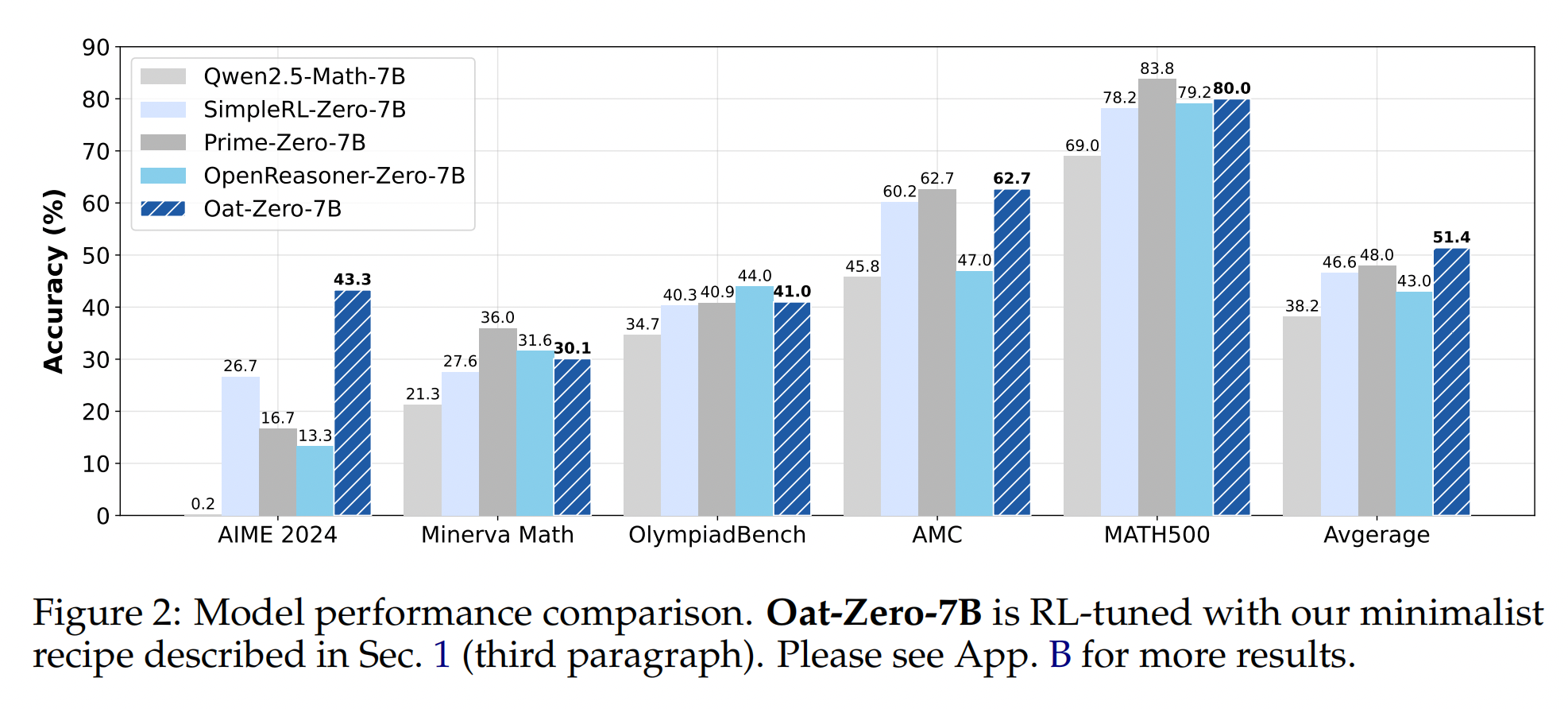
我们对基础模型和强化学习 (RL) 的分析表明,R1-Zero 训练存在一种极简方案:我们使用 (无偏) Dr. GRPO 算法,在 MATH (Hendrycks et al., 2021) 数据集难度等级 3-5 的问题上,利用 Qwen-Math 模板对 Qwen2.5-Math-7B 进行强化学习微调。仅使用 8 × A100 GPU 上 27 小时的计算,我们就实现了最先进的性能(图 2)。
关键要点的概述
- (第 2.1 节) 模板对于使基础模型回答问题而不是完成句子至关重要。此外,所有基础模型在强化学习 (RL) 之前已经具备数学求解能力。
- (第 2.2 节) 有趣的是,Qwen-2.5 基础模型在不使用模板的情况下立即获得了约 60% 的改进,这让我们假设它们在训练模型时可能预训练了连接的问题-答案文本。
- (第 2.3 节) 几乎所有基础模型都表现出“灵光一现”,包括 DeepSeek-V3-Base。
- (第 3.1 节,第 3.2 节) Dr. GRPO 有效地修复了 GRPO 在优化中的偏差,从而实现了更好的 Token 效率。
- (第 3.3 节) 模型-模板不匹配可能会破坏推理能力,然后强化学习 (RL) 会重建它。
- (第 3.4 节) 在 Llama-3.2-3B 上进行数学预训练可以提高其强化学习 (RL) 的上限。
2 基础模型分析
在本节中,我们仔细研究了各种基础模型,包括 Qwen-2.5 系列 、Llama-3.1和 DeepSeek 系列 。我们从 MATH 训练集中抽取了 500 个问题,并向这些模型提问,然后分析它们的回答。
2.1 R1-Zero 可训练性:模板构建探索性基础策略
由于从基础模型进行训练是类 R1-Zero 范式的基本设置,我们首先研究广泛使用的开源基础模型(通常针对句子补全进行训练,即 $p_\theta(x)$是否可以通过适当的模板有效地激发其问答能力,从而充当问答基础策略$\pi_\theta(|q)$。除了 Guo et al. (2025) 中的 R1 模板(模板 1)之外,我们还考虑了 Zeng et al. (2025) 使用的 Qwen-Math 模板(模板 2),以及无模板(模板 3):

实验设置
我们纳入了 Qwen2.5-Math-1.5B、Qwen2.5-Math-7B、Qwen2.5-7B、Llama-3.1-8B、DeepSeek-Math-7B 和 DeepSeek-V3-Base-65B 用于实验。对于每个模型,我们首先应用“无模板” (No template) 来获取模型响应,然后使用 GPT-4.0 来判断模型响应是否为回答问题的格式(不考虑质量),或者为句子补全模式。我们将倾向于回答问题的响应百分比记录为指标。然后,我们应用 R1 模板和 Qwen-Math 模板来获取模型响应,并根据该指标确定每个模型最合适的模板。最后,我们使用相应的模板评估每个模型的 pass@8 准确率,以评估基础策略是否可以探索用于强化学习改进的奖励轨迹。
结果
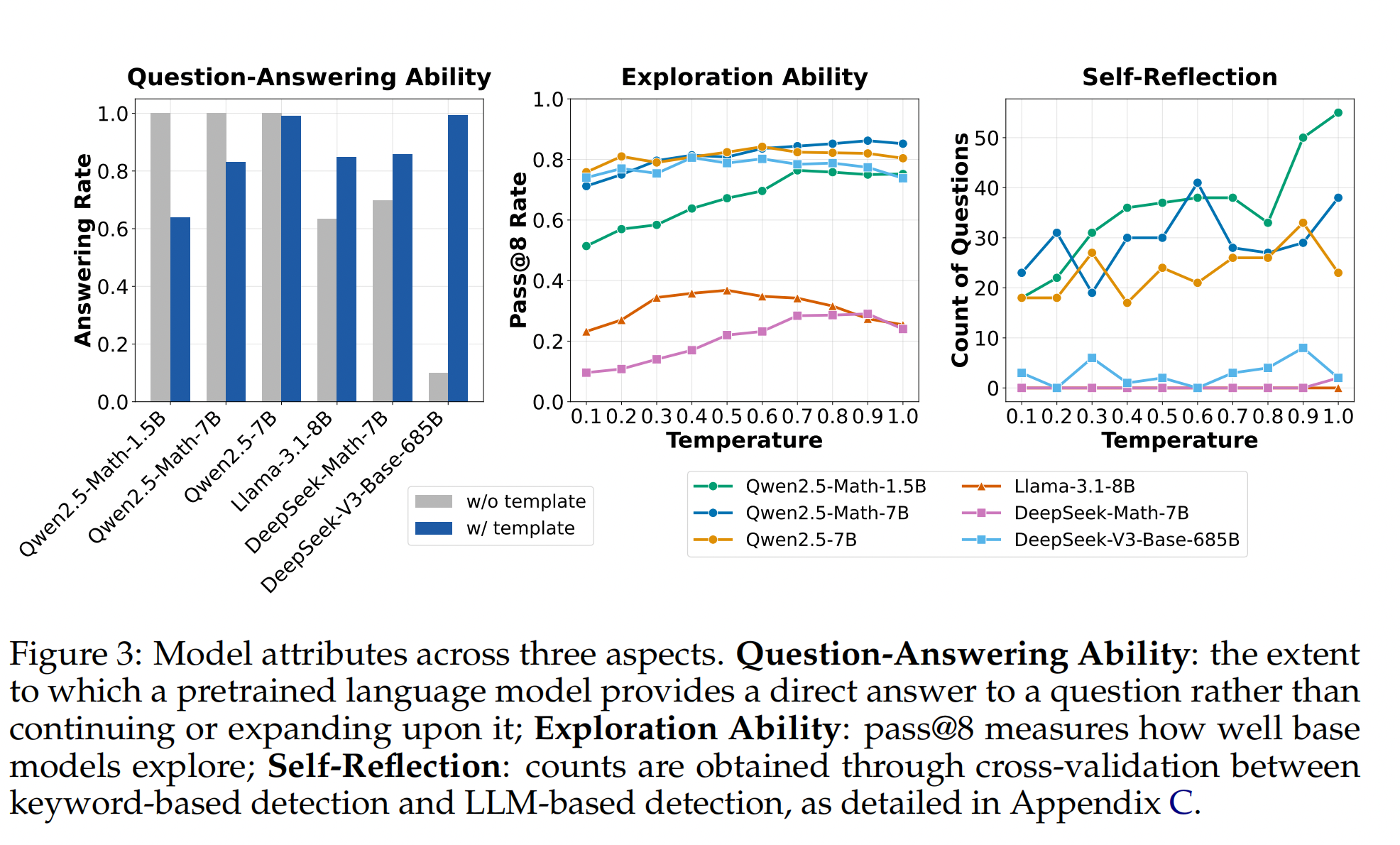
图 3 的左图显示了基础模型(无论是否使用模板)回答所提供问题的效果。我们观察到,Llama 和 DeepSeek 模型都通过使用适当的模板(R1 模板)提高了回答能力。然而,Qwen2.5 模型在不使用模板时效果最佳(回答率达到 100%)。这种有趣的特性促使我们进一步研究,如第 2.2 节所述。同时,在不使用模板时最低的回答率表明 DeepSeek-V3-Base 是一个几乎纯粹的基础模型。这一观察结果促使我们探索像 DeepSeek-V3-Base 这样的纯粹基础模型是否会表现出 Aha 时刻。图 3 的中间图显示了不同基础模型(使用模板)在不同采样温度下的 pass@8 通过率。该指标可以作为基础策略探索能力的指标。例如,如果一个策略甚至无法采样到一条能够得到正确最终答案的轨迹,那么强化学习就不可能改进该策略,因为没有奖励信号。我们的结果表明,所有测试的模型都具有探索性(因此可以进行强化学习),其中 Qwen2.5 模型表现最佳(甚至超过了 DeepSeek-V3-Base)。这可能部分解释了为什么大多数 R1-Zero 项目)都基于 Qwen2.5 模型。
2.2 Qwen2.5 模型:舍弃模板释放最佳性能
接下来,我们将深入研究一个有趣的现象(参见图 3 左图):所有 Qwen2.5 基础模型在不使用任何模板的情况下,都能直接发挥其应有的性能。我们将更进一步进行评估。
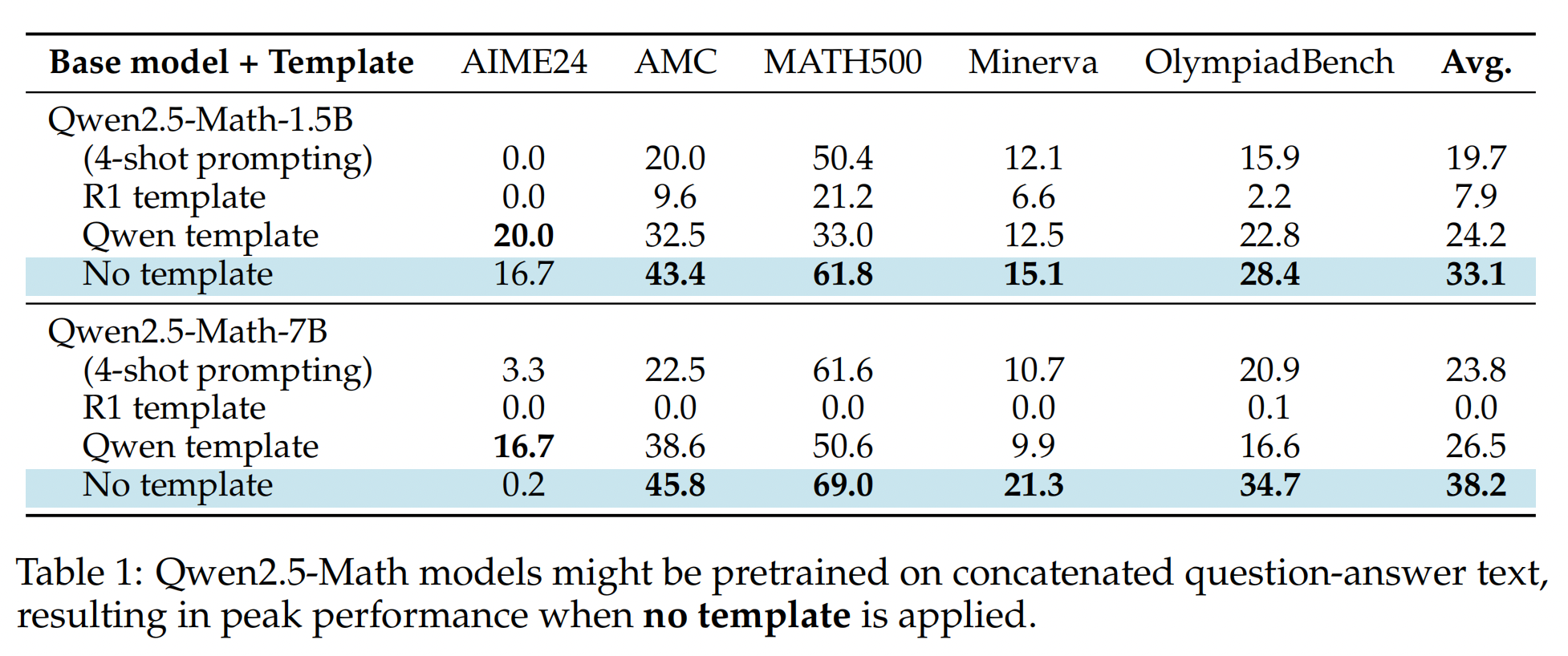
如表1所示,不使用任何模板可以显著提高平均性能,与传统的少样本学习提示相比,提升幅度约为60%。由于Qwen2.5-Math在预训练阶段使用了该模型的数据(问题-答案对),我们假设他们可能在拼接的文本上进行预训练,以直接最大化 $log p(q;θ)$。如果我们的假设被证实,我们在使用Qwen2.5模型复现DeepSeek-R1-Zero时应更加谨慎,因为基础模型已经类似于没有模板的SFT。
2.3 “顿悟时刻”已出现在包括 DeepSeek-V3-Base 在内的基础模型中
DeepSeek-R1-Zero 最鼓舞人心的结果之一是通过纯粹的强化学习训练涌现出的自我反思行为,也就是所谓的“顿悟时刻”。此前的一些研究表明,开源强化学习训练中可能不存在“顿悟时刻”,因为他们使用的基础模型已经表现出自我反思的关键词。然而,他们没有测试 DeepSeek-V3-Base,而真正的 R1-Zero 模型正是在此基础上进行强化学习微调的。我们通过托管 DeepSeek-V3-Base-685B 来补全这缺失的一环。从图 3 的右图中,我们可以观察到 DeepSeek-V3-Base 也生成了相当数量的自我反思,进一步验证了 Liu 等人 (2025b) 的说法。我们还在图 4 中展示了 DeepSeek-V3-Base 生成诸如“Aha”、“wait”和“veR1fy the problem”等关键词的例子。

另一个重要的问题是,自我反思行为是否能提高 RL 训练后的模型性能。为了研究这一点,我们托管了 DeepSeek-R1-Zero,并分析了它对 MATH 数据集中相同问题的回答。我们发现自我反思行为在 R1-Zero 中更频繁地出现。然而,没有明确的证据表明它们与更高的准确性相关。
3. 强化学习分析
语言模型生成可以被形式化为一个 Token 级别的马尔可夫决策过程 (MDP) $M = (S, A, r, p_{\mathcal{Q}})$ 。在每个生成步骤 $t$,状态$s_t \in S$ 是输入问题和到目前为止生成的输出响应的连接:
$s_t=q;o_{ 策略$\pi_\theta(s_t)$将从词汇表A 中选择下一个 Token,从而确定性地转移到下一个状态$s_{t+1} = s_t ;[o_t]$。生成过程从问题集合中采样一个初始状态 $s_1 = q \sim p_Q$开始,并在自回归策略生成 [EOS] Token 或耗尽预算时停止。
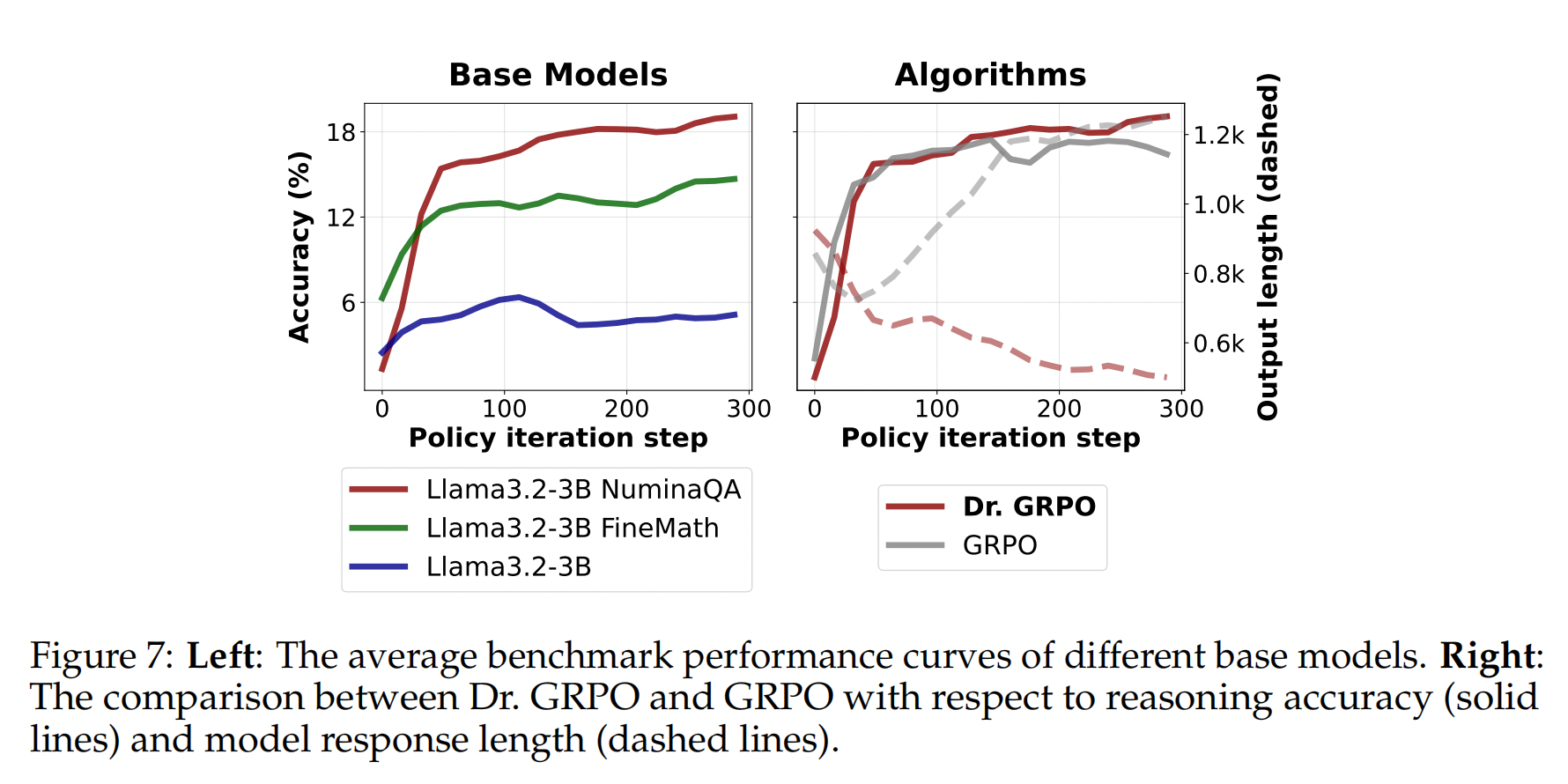
通常,我们最大化熵正则化目标 其中$R(q,o) = \sum_{t=1}^{|o|} r(s_t, o_t)$是轨迹$q;o$的回报 ,而$\pi_{ref}$是参考策略。KL 正则化项通常被采用 ( $\beta > 0$ ) 用于从人类反馈中进行强化学习 ),其中 $r$ 是奖励。 模型从由 $\pi_{ref}$ 收集的数据中学习。在这种情况下,正则化有助于防止 $π_θ$ 偏离奖励模型准确的分布过远。然而,在使用强化学习 (RL) 微调推理模型时,通常采用基于规则的验证器 $r$,这消除了对分布偏移的担忧。因此,我们可以移除 KL 项,这不仅节省了 $\pi_{ref}$ 在训练期间所需的内存和计算资源,而且还可能为类似 R1-Zero 的训练带来更好的性能 。在本文中,我们将始终假设 $β = 0$。 策略优化算法 为了使用上述目标,其中 $β = 0$)优化 $π_θ$,近端策略优化 (PPO) 最大化以下替代目标: 其中 $\pi_{\theta_{\text {old }}}$ 是更新前的策略,$ε$ 是裁剪超参数,$\hat{A}_t$是第 $i$ 个 Token 的优势函数估计值。估计$\hat{A}_t$ 的一种标准方法是使用学习到的价值模型 $V_\phi$ 计算广义优势估计 (GAE) 。然而,在大语言模型 (LLM) 强化学习 (RL) 微调的上下文中,学习价值模型计算成本很高,因此实际上更倾向于在没有 $V_\phi$ 的情况下估计 $\hat{A}_t$ 的方法。例如,Shao 等人 (2024) 提出了 GRPO,它首先为每个问题采样一组响应 $\{o₁, …, o_G\}$,并计算它们的收益 $R = \{R₁, …, R_G\}$,然后将来自$o_i$ 的所有 Token 的优势设置为:$\hat{A}_t=\frac{R_i-\operatorname{mean}(\mathbf{R})}{\operatorname{std}(\mathbf{R})} .$ 其中 $R(q | o_i)$ 表示给定问题 $q$ 和 Deepseek-R1-Zero 中采样的响应 $o_i$ 的结果奖励(该结论也适用于过程奖励的情况)。与公式 (2) 中的目标函数相比: 长度偏差也存在于开源PPO实现中 我们还检查了几个流行的用于大语言模型(LLM)后训练的原始PPO算法的开源实现。令我们惊讶的是,所有这些实现都表现出损失中基于响应长度的偏差(参见列表 1 和表 2),即使在 GRPO 发布之前就存在。我们推测,这种每个 Token 的归一化源于大语言模型(LLM)的下一个 Token 预训练,其中旨在使每个 Token 对目标做出同等贡献。然而,在强化学习的背景下,通过除以 $|o_i|$ 进行归一化会引入一个意想不到的偏差。 为了避免 GRPO 中提到的优化偏差,我们建议简单地移除 $\frac{1}{|o_i|}$和 $std(R(q, o_1), \ldots, R(q, o_k)$归一化项。同时,为了实现无偏优化目标,我们可以用一个常数值(例如,生成预算)替换清单 1 中 masked.mean 函数中的 mask.sum(axis=dim),如绿色行突出显示的那样。值得注意的是,这些简单的修改恢复了 Eq. (2) 中的 PPO 目标,其优势由具有无偏基线的蒙特卡罗回报估计。我们将我们的新优化算法称为 Dr. GRPO。接下来,我们将通过实验验证 Dr. GRPO 的有效性。 我们使用 Oat 来实现我们的算法,Oat 是一个模块化、对研究友好且高效的 大语言模型 (LLM) 强化学习框架。我们采用 Qwen2.5-1.5B 基础模型和 R1 模板(模板 1)进行在线强化学习 fine-tuning。我们使用 Math-VeR1fy² 实现基于验证的奖励函数,采用以下最小化规则: 我们在从 MATH 训练数据集中抽样的问题上运行强化学习 (RL),并将原始 GRPO 与我们提出的 Dr. GRPO 进行比较。我们在五个基准测试上评估在线模型:AIME2024、AMC、MATH500、Minerva Math 和 OlympiadBench。包括超参数在内的更多实验细节可以在我们的开源代码库中找到。 我们在图 5 中报告了各项指标,以证明 Dr. GRPO 能够有效缓解优化偏差,并提升 Token 效率。 特别是,我们首先注意到 GRPO 和 Dr. GRPO 都表现出与 DeepSeek-R1-Zero 相似的趋势,即它们的响应长度随着训练奖励的增加而增加(图 1 和图 2)。 然而,我们观察到,即使奖励提升的速度减缓,GRPO 仍倾向于持续生成更长的响应(图 2)。 尽管这种现象通常被称为通过 RL 实现 long-CoT 的“涌现”),但我们认为它也受到优化过程中响应级别的长度偏差(第 3.1 节)的影响。 相比之下,通过计算无偏策略梯度,Dr. GRPO 能够防止响应长度在训练期间过度增长(图 2)。 此外,在评估基准上,与基线相比,Dr. GRPO 显著减少了错误响应的长度(图 4),这表明无偏优化器也能缓解过度思考。 回想一下,Qwen2.5-Math 基础模型无需任何提示词模板即可轻松且高精度地回答问题。 基于这一有趣的观察,我们对不同的模板如何影响强化学习 (RL) 训练很感兴趣。 此外,鉴于普遍认为更大的问题集覆盖范围会带来更好的性能,我们还研究了不同模板和不同问题覆盖水平之间的相互作用。 从 Qwen2.5-Math-1.5B 基础模型开始,我们分别应用 R1 模板、Qwen-Math 模板和无模板,使用 Dr. GRPO 运行强化学习。所有实验针对表 3 中详细说明的不同问题集重复进行。 请注意,Zeng et al. (2025) 和 Hu et al. (2025) 都采用了 PPO,它在公式上是无偏的。然而,他们的损失函数实现仍然引入了长度偏差(参见列表 1)。 图展示了不同运行的强化学习 (RL) 曲线,从中我们可以得出几个有趣的观察结果: 最近,在数学推理器上成功复现的类 RL-Zero 方法,大多采用 Qwen2.5 基础模型作为初始策略。这些模型本身已是强大的数学问题求解器,并展现出自反思的特性(第 2.2 节和 2.3 节)。本节旨在探索另一个方面:在数学推理能力较弱的基础模型上,类 R1-Zero 的训练是否也能成功? 我们的实验给出了肯定的答案,并观察到数学领域的预训练能够有效提升强化学习(RL)的性能上限。 实验设置。 我们选择 Llama-3.2-3B 作为基础模型,并采用无偏的 Dr. GRO 算法,结合 R1 模板进行强化学习微调。 基于领域特定预训练能够提升 RL 性能的假设,我们采用了 Llama-3.2-3B-FineMath4 模型,该模型在 FineMath 数据集上进行了持续预训练。 此外,考虑到 Qwen2.5 模型可能使用了拼接的问题-答案文本进行预训练(第 2.2 节),我们同样从 NuminaMath-1.5 数据集中构建了一个拼接数据集,并使用该数据集对 Llama-3.2-3B-FineMath 模型进行了 2 个 epoch 的持续预训练,并调整了学习率。 我们将这个经过拼接数据集持续预训练的模型命名为 Llama-3.2-3B-NuminaQA。 我们在图 7 的左图中展示了不同基础模型的 RL 曲线。我们观察到,强化学习 (RL) 甚至可以改进原始的 Llama 基础模型,但增益很小。在经过持续预训练(以及串联的持续预训练)以嵌入数学领域之后。 我们以批判性的视角审视了用于 R1-Zero 类似训练的基础模型,以及用于强化学习的算法。通过分析,我们揭示了预训练偏差如何影响强化学习的结果,以及像 GRPO 这样的优化选择如何无意中塑造模型的行为。通过我们提出的 Dr. GRPO,我们提供了一个简单的修复方案,可以在保持推理性能的同时提高 Token 效率。我们的结果表明,扩展强化学习既有效率又有效——有时候,少即是多。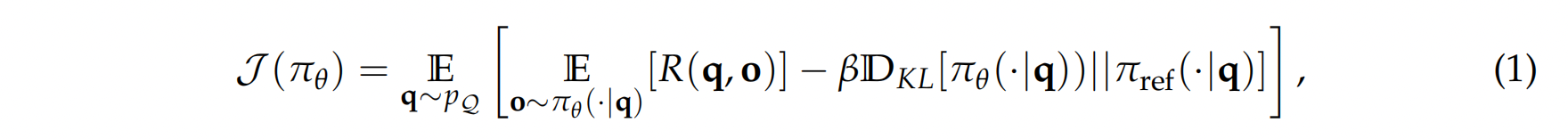
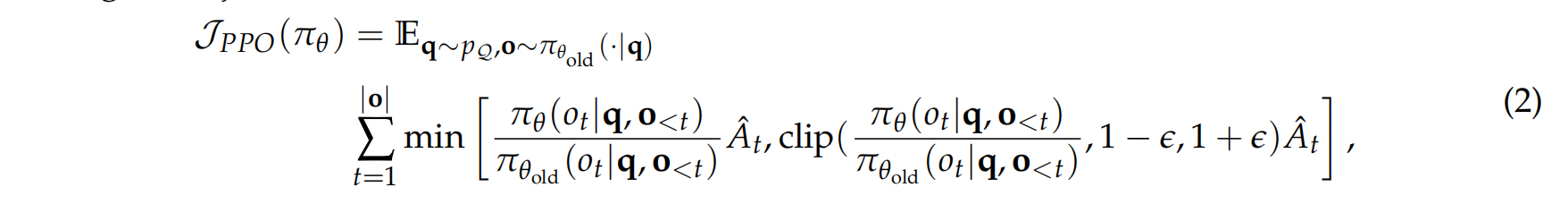
3.1GRPO 引入了两个偏差
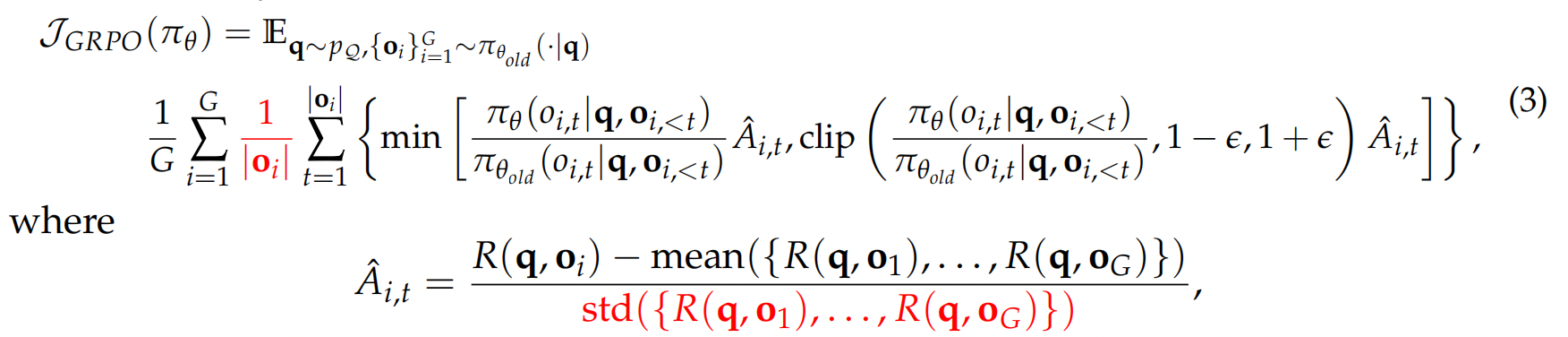

3.2 Dr. GRPO:正确完成的GRPO
实验设置

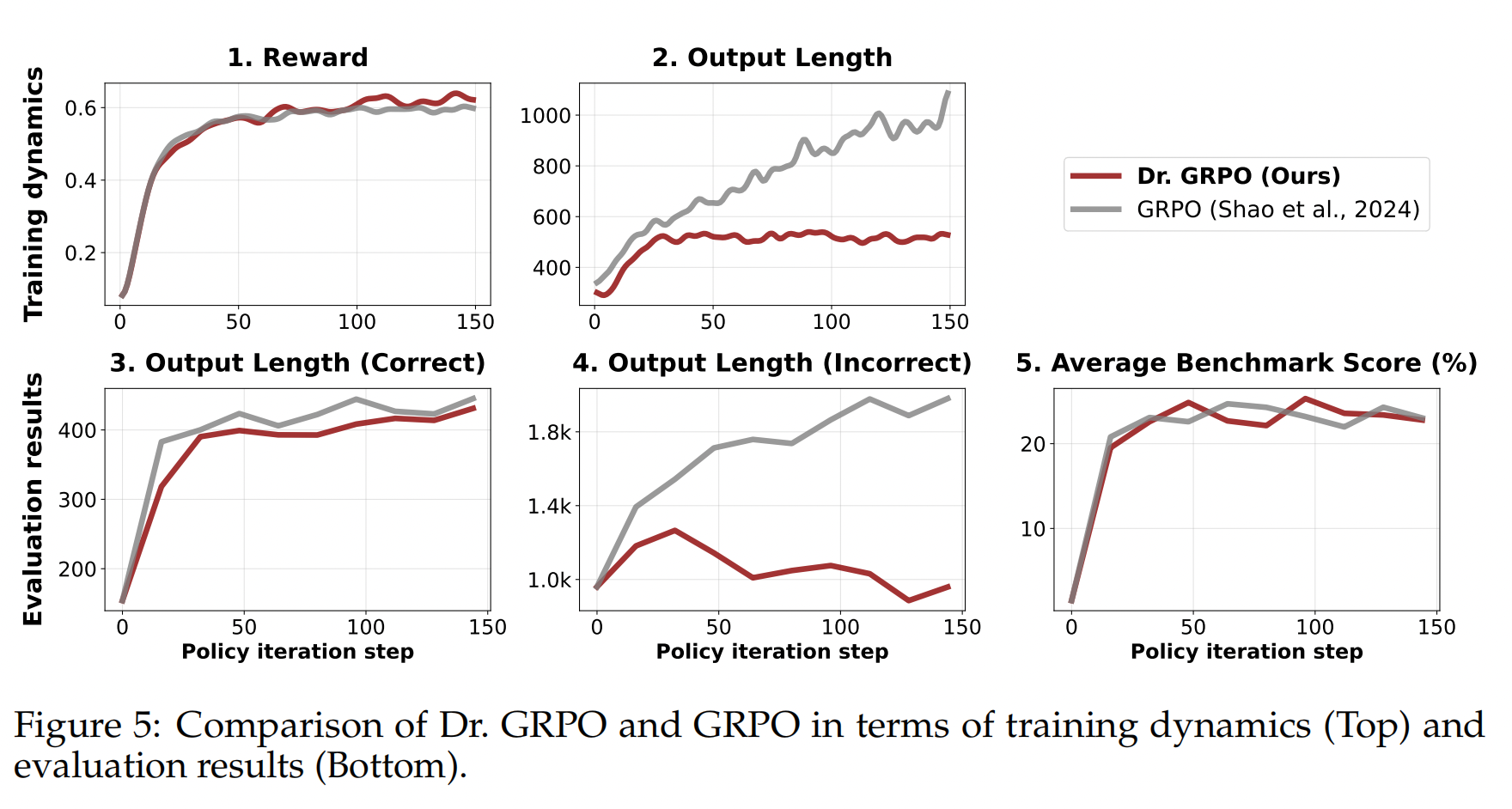
结果
3.3 RL 动态中的模板与问题集覆盖的双重奏
实验设置

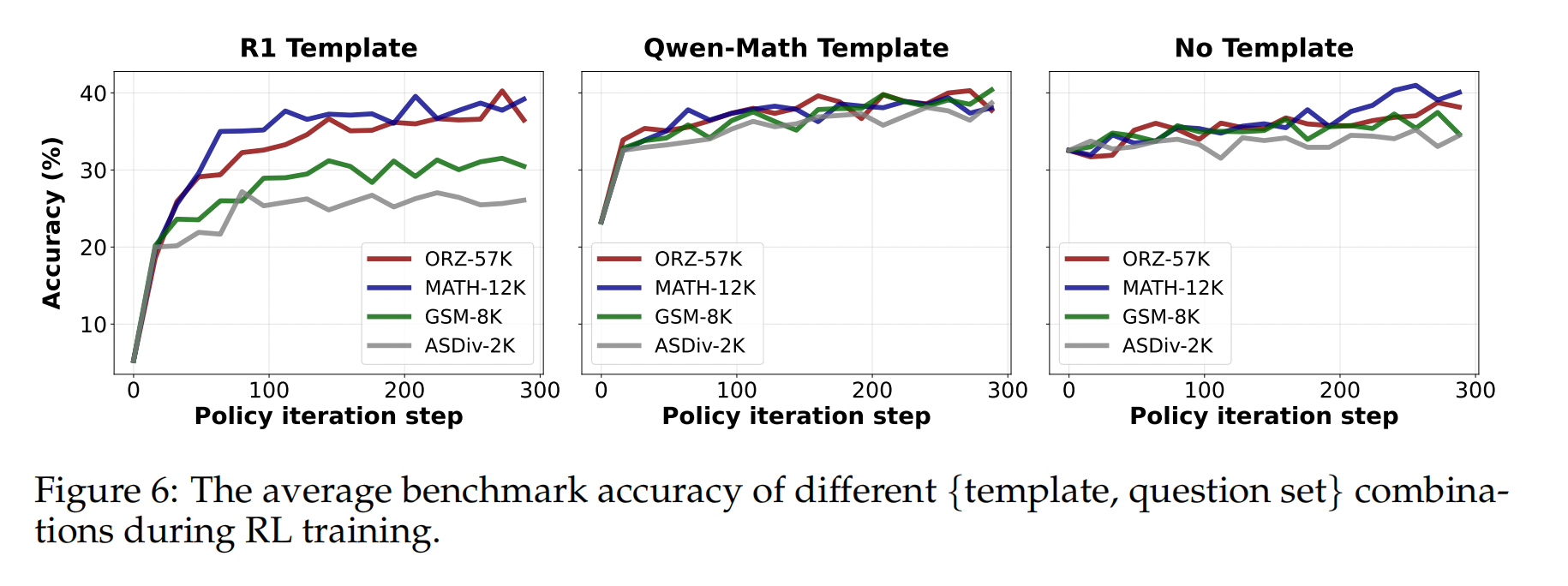
结果.
3.4 领域特定预训练提升 RL 上限
结果
4 结束语
