Unsloth的梯度累积修复确保训练过程和损失计算能够准确和正确地执行。梯度累积的目标是在减少显存(VRAM)使用量的同时模拟完整批次训练。由于梯度累积也用于DDP和多GPU设置中,因此这个问题同样影响着大规模训练。
from unsloth import unsloth_train
# trainer_stats = trainer.train() << 存在bug的梯度累积
trainer_stats = unsloth_train(trainer)
复现问题
理论上,梯度累积在数学上应该等效于完整批次训练。我们使用有效批次大小16进行训练,因此批次大小(bsz) * 梯度累积步数(ga)应保持恒定。我们测试了bsz=1,2,4,8和16,发现使用较大梯度累积步数的训练损失始终更高。
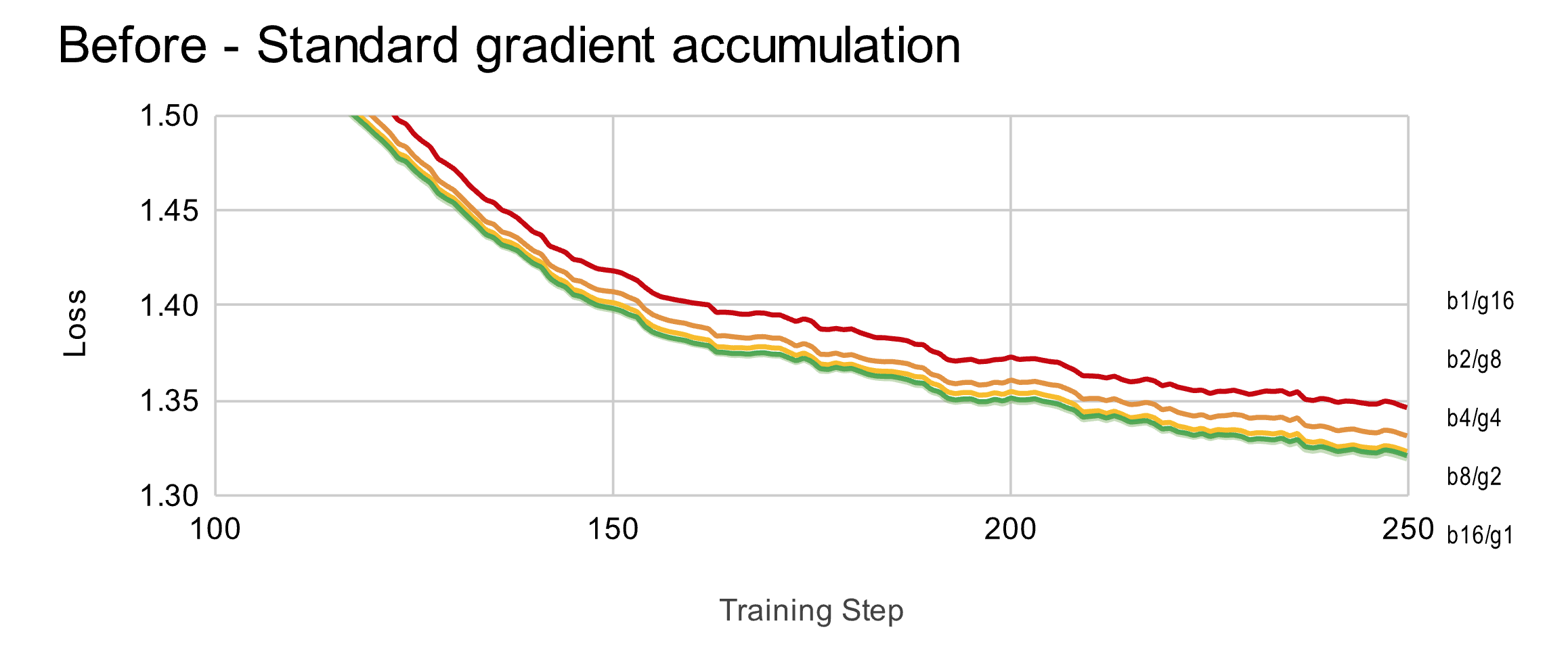
什么是梯度累积?
在训练或微调过程中,每一步都会从训练数据集中选择一定数量的随机样本来更新模型权重。但应该选多少样本呢?对于非常大的预训练任务,批次大小可能达到数百万,就像在Llama 3.1中那样,这有助于减少过拟合并提高模型的泛化能力。而对于像Unsloth的Llama 3.2笔记本中的微调任务,批次大小可能只有较小的32。

问题在于大批次的内存使用量非常大。如果1个批次使用1单位内存,那么100万大小的批次将需要100万单位内存。我们如何模拟大批次训练但又不消耗大量内存呢?
这就是梯度累积的用武之地!我们通过在每次新的小批次到来时即时创建梯度,然后将所有小梯度加起来,进行适当缩放,从而获得最终的大批次梯度。
可能的解释
一种流行的理论认为梯度累积在累积步骤中存在数值误差。但研究人员发现,即使在float32中进行累积也会产生相同的问题。我们的研究表明,确实存在一些微小的累积误差。
第二种理论是损失计算中存在bug,我们确认了这一点。
数学上是否等价?
梯度累积和完整批次训练在数学上是否等价?遗憾的是,如果简单地将梯度加起来,答案是否定的!我们首先注意到交叉熵损失是通过以下方式计算的:
$$ \frac{1}{\sum \mathbb{I}\{y_i \neq -100\}} \sum L_i $$注意分母计算的是非填充或非忽略的token数量 - 即它通过每个文本片段中有效训练token的数量来归一化损失。指示函数实际上是未填充token的总和,也就是所有序列长度的总和,即:
$$ \mathbb{I}\{y_i \neq -100\} = \sum m_i $$因此我们得到最终方程为:
$$ \frac{\sum L_i}{\sum m_i} $$然后我们在分子和分母中同时添加 $\frac{1}{n}$ - 这是允许的,因为两者可以相互抵消:
$$ \frac{\frac{1}{n}\sum L_i}{\frac{1}{n}\sum m_i} $$这意味着最终损失是平均损失值除以所有未填充序列长度的平均值:
$$ \frac{\bar{L}}{\bar{m}} $$在进行梯度累积时,我们需要分别计算每个小批次的损失,然后将它们加起来得到最终损失。我们首先利用每个分区的平均损失和平均序列长度。
但我们发现,最终总和不等于原始的完整批次损失 - 实际上它比原来大$G$倍(其中$G$是梯度累积步骤的数量)。
$$ L = \sum \left[ \frac{L_1}{m_1} | \frac{L_2}{m_2} | \frac{L_3}{m_3} | \frac{L_4}{m_4} \right] $$$$ L = \sum \left[ \frac{\bar{L}}{\bar{m}} | \frac{\bar{L}}{\bar{m}} | \frac{\bar{L}}{\bar{m}} | \frac{\bar{L}}{\bar{m}} \right] $$$$ L = G \cdot \frac{\bar{L}}{\bar{m}} \neq \frac{\bar{L}}{\bar{m}} $$因此在梯度累积中,我们必须按梯度累积步骤的数量G来缩放每个小梯度累加器,才能得到期望的结果。
$$ L = \sum \left[ \frac{1}{G} \cdot \frac{L_1}{m_1} | \frac{1}{G} \cdot \frac{L_2}{m_2} | \frac{1}{G} \cdot \frac{L_3}{m_3} | \frac{1}{G} \cdot \frac{L_4}{m_4} \right] $$这对于大批次的期望值通常效果良好。
==但是,如果不同批次的序列长度不同会发生什么 - 这难道不会导致问题吗?==
为了验证这一点,我们通过完全移除分母进行测试 - 即不使用归一化的交叉熵损失,而是简单地使用未归一化的损失来确认梯度累积是否仍然有效。修改后的Unsloth训练运行中的训练损失如下:
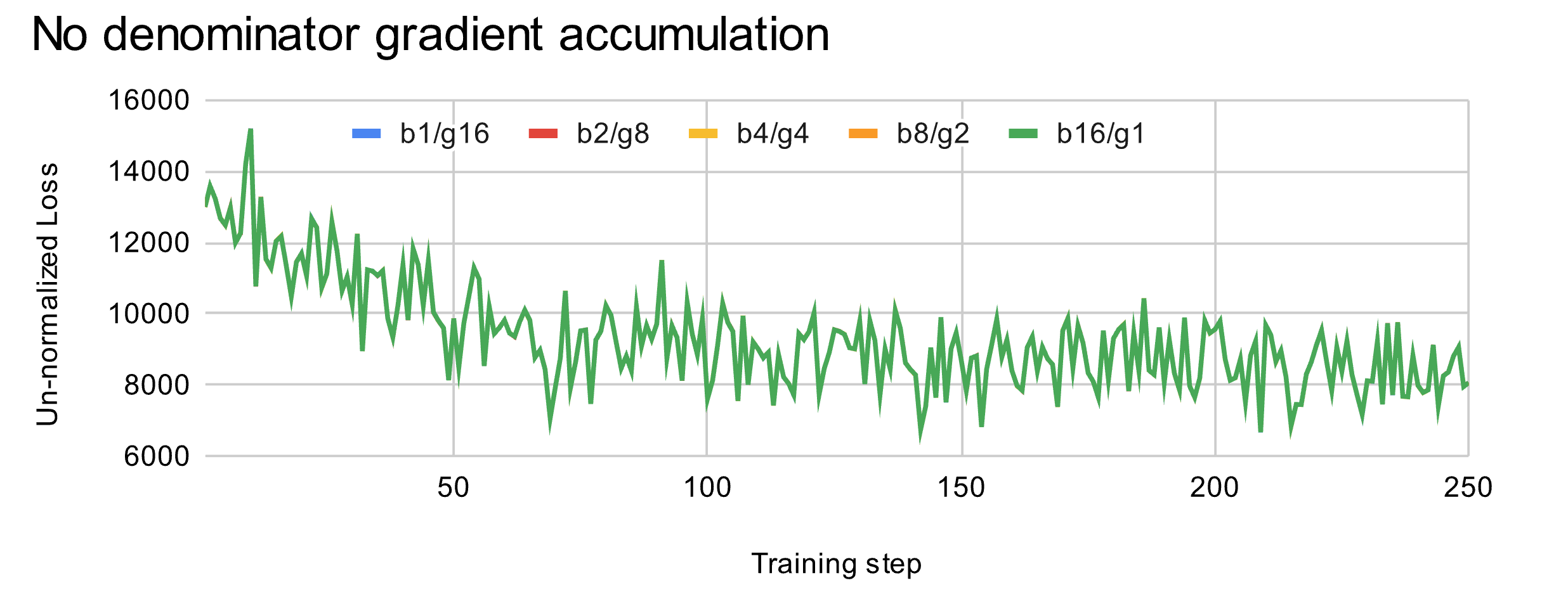
神奇的是,我们看到所有训练损失曲线都完美匹配!这意味着分母确实是罪魁祸首!这表明简单地对每个梯度累积步骤进行平均是错误的,正确的做法是我们必须事先推导分母。
我们在Unsloth中实现了这个修复,现在所有损失曲线都匹配一致,证明了梯度累积确实等同于完整批次训练。
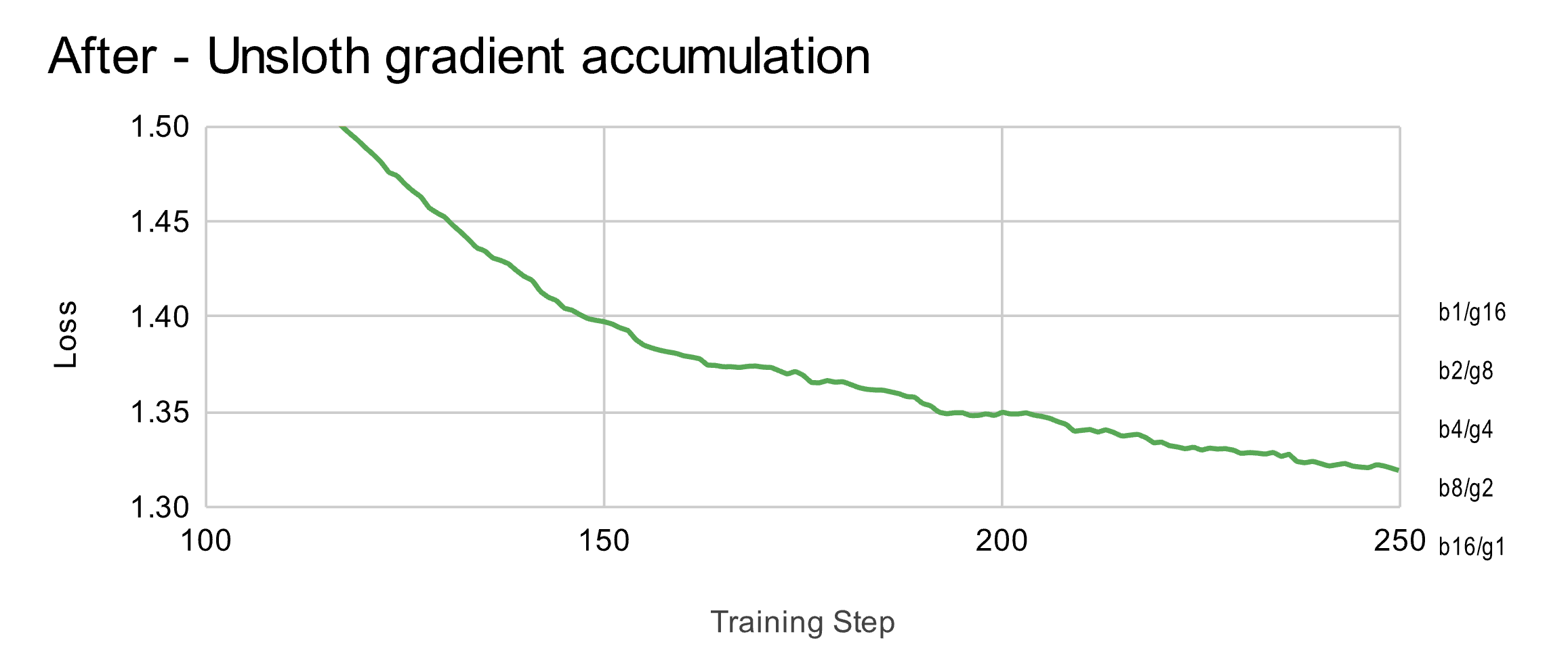
数值差异
另一个需要考虑的问题是,这个错误是否会实际影响最终权重的差异。为此,我们使用Unsloth训练了一个LoRA适配器,分别使用完整批次(bsz=16,ga=1)和仅使用梯度累积的版本(bsz=1,ga=16)。
我们运行了所有组合(从bsz=1,ga=16到bsz=16,ga=1),并将这些LoRA权重与完整批次版本(bsz=16,ga=1)进行比较,计算L2范数差异。
我们发现:(1)由于浮点算术计算,确实存在固有的累积误差(0.0068 L2范数),以及(2)随着梯度累积数量的增加,L2范数差异也增加(从0.0196到0.0286 L2范数)
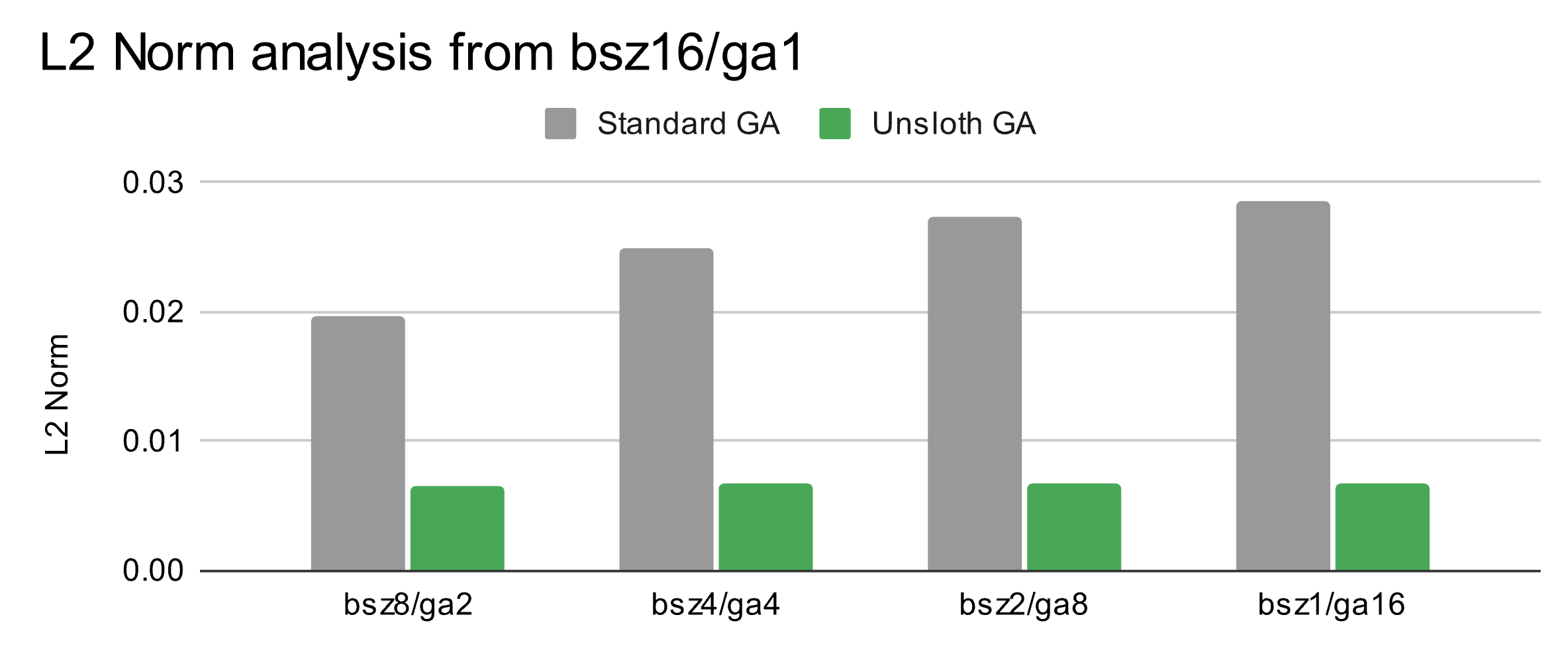
这本质上意味着梯度累积本身确实存在微小的浮点加法惩罚。而且,梯度累积步骤越多,差异越大。通过使用我们修复后的Unsloth梯度累积版本,L2范数误差可以减少一个数量级以上。
附加内容 - 数学证明
假设我们有批次大小为2和梯度累积步数为2,那么分别在无梯度累积(完整批次训练)和有梯度累积的情况下的最终损失如下所示:
$$ L = \frac{L_1 + L_2 + L_3 + L_4}{m_1 + m_2 + m_3 + m_4} $$$$ L = \frac{1}{2} \cdot \frac{L_1 + L_2}{m_1 + m_2} + \frac{1}{2} \cdot \frac{L_3 + L_4}{m_3 + m_4} $$$$ \frac{1}{2} \cdot \frac{L_1 + L_2}{m_1 + m_2} + \frac{1}{2} \cdot \frac{L_3 + L_4}{m_3 + m_4} \\ \geq \frac{L_1 + L_2 + L_3 + L_4}{m_1 + m_2 + m_3 + m_4} $$然后我们以类似的方式证明另一个不等式方向。我们注意到,与其直接证明,如果我们能证明比率大于1,也可以达到同样的证明效果。我们之所以能这样做,是因为我们知道序列长度 $m$ 始终大于0。我们还使用平均损失进行计算。
$$ \frac{\frac{1}{2} \cdot \frac{L_1 + L_2}{m_1 + m_2} + \frac{1}{2} \cdot \frac{L_3 + L_4}{m_3 + m_4}}{\frac{L_1 + L_2 + L_3 + L_4}{m_1 + m_2 + m_3 + m_4}} \geq 1 $$$$ \frac{\frac{1}{2} \cdot \frac{2 \cdot \bar{L}}{m_1 + m_2} + \frac{1}{2} \cdot \frac{2 \cdot \bar{L}}{m_3 + m_4}}{\frac{4 \cdot \bar{L}}{m_1 + m_2 + m_3 + m_4}} \geq 1 $$通过简化和一些代数运算,我们得到:
$$ \frac{\left(\frac{1}{2} \cdot \frac{2 \cdot \bar{L}}{m_1 + m_2} + \frac{1}{2} \cdot \frac{2 \cdot \bar{L}}{m_3 + m_4}\right) \cdot (m_1 + m_2 + m_3 + m_4)}{4 \cdot \bar{L}} \geq 1 $$$$ \frac{\left(\frac{\bar{L}}{m_1 + m_2} + \frac{\bar{L}}{m_3 + m_4}\right) \cdot (m_1 + m_2 + m_3 + m_4)}{4 \cdot \bar{L}} \geq 1 $$$$ \frac{(m_3 + m_4) \cdot \bar{L} + (m_1 + m_2) \cdot \bar{L}}{(m_1 + m_2) \cdot (m_3 + m_4)} \cdot \frac{m_1 + m_2 + m_3 + m_4}{4 \cdot \bar{L}} \geq 1 $$$$ \frac{1}{4} \cdot \frac{(m_1 + m_2 + m_3 + m_4)^2}{(m_1 + m_2) \cdot (m_3 + m_4)} \geq 1 $$$$ (m_1 + m_2 + m_3 + m_4)^2 \geq 4 \cdot (m_1 + m_2) \cdot (m_3 + m_4) $$现在假设所有序列长度都相同。在这种情况下,我们应该期望完整批次训练与梯度累积得到相同的结果。
$$ (m + m + m + m)^2 \geq 4 \cdot (m + m) \cdot (m + m) $$$$ 16m^2 \geq 16m^2 $$我们可以看到,得到了预期的结果 - 完整批次训练和梯度累积确实是相同的!但是,如果有1个序列长度(仅1个)比其他序列长度大一个小的ε值,会发生什么?
$$ (4m)^2 \geq 4 \cdot (2m) \cdot (2m) $$$$ (4m + \epsilon)^2 \geq 4 \cdot (2m + \epsilon) \cdot (2m) $$$$ 16m^2 + 8m\epsilon + \epsilon^2 \geq 16m^2 + 8m\epsilon $$我们看到有一个ε平方项,它总是大于0!但是,我们还需要证明如果有1个序列长度略小于其他序列长度,这个结论也成立:
$$ (4m)^2 \geq 4 \cdot (2m) \cdot (2m) $$$$ (4m - \epsilon)^2 \geq 4 \cdot (2m - \epsilon) \cdot (2m) $$$$ 16m^2 - 8m\epsilon + \epsilon^2 \geq 16m^2 - 8m\epsilon $$在这两种情况下,不等式都成立,因为我们知道ε平方是一个总是大于或等于0的数。这本质上证明了对于bsz=2和ga=2的情况,简单或标准的梯度累积总是比完整批次训练有更高的损失。然后,我们可以将这个证明推广到bsz和ga的其他组合,虽然证明过程可能会变得更加复杂。
我们还必须证明不等式在另一个方向也成立 - 即最终目标是证明一般的简单梯度累积与完整批次训练在数学上是不等价的。
